Το βαρυτικό πρόβλημα των δύο κέντρων

Που μπορεί να σε φτάσει η απορία ενός μαθητή: μετά τους προβληματισμούς μου σχετικά με τις τροχιές στο πρόβλημα των δύο σωμάτων όταν βαρυτική δύναμη δεν ακολουθεί επακριβώς το νόμο του αντιστρόφου τετραγώνου (βλ. προηγούμενη ανάρτηση), ασχολήθηκα στον ελεύθερο χρόνο μου γενικά με προσομοιώσεις βαρυτικών συστημάτων, ανακαλύπτοντας κυρίως πράγματα ήδη γνωστά σε όσους ασχολούνται με το αντικείμενο. Καταχράστηκα μάλιστα τον υπολογιστικό μου χρόνο σε ένα μεγάλο υπολογιστή του πανεπιστημίου (ελπίζω ο διαχειριστής του συστήματος να μη με διαβάζει) και έτρεξα μια προσομοίωση ενός μίνι ηλιακού συστήματος, υπολογίζοντας τροχιές, εκθέτες Lyapunov (μέτρο της αστάθειας ενός συστήματος) και την εξάρτησή τους από κάποιες παραμέτρους, μεταξύ των οποίων και η μορφή του νόμου της βαρυτικής έλξης. Επιπλέον, ασχολήθηκα και με άλλα δυναμικά δύο κέντρων χωρίς όμως τον απειρισμό της βαρυτικής δύναμης στο κέντρο, όπως για παράδειγμα δύο πηγάδια δυναμικού της μορφής

.

Τα αποτελέσματα είναι ενδιαφέροντα και κάποια από αυτά πρωτότυπα και θα τα αναφέρω σε άλλη δημοσίευση. Εδώ θα γράψω λίγα λόγια για το πρώτο βήμα στη διαδρομή από το πρόβλημα των δύο σωμάτων σε εκείνο (το απείρως πολυπλοκότερο) των τριών: το πρόβλημα των δύο κέντρων, χωρίς να σκοπεύω να γράψω κάτι περισσότερο σε σχέση με την υπάρχουσα βιβλιογραφία. Απλώς θα τα γράψω πιο περιγραφικά, κατανοητότερα για το μη ειδικό και πιο κοντά στον τρόπο που τα κατάλαβα εγώ.

Αντί λοιπόν να έχουμε ένα σωματίδιο να αλληλεπιδρά βαρυτικά με ένα άλλο, έχουμε ένα σωματίδιο να αλληλεπιδρά με δύο άλλα, τα οποία όμως θεωρούμε ακίνητα. Αδύνατο βέβαια να πραγματοποιηθεί κάτι τέτοιο στη φύση (δύο σώματα που έλκονται βαρυτικά είναι αδύνατο να μένουν ακίνητα το ένα ως προς το άλλο) αλλά είναι ένα πρώτο βήμα αύξησης της πολυπλοκότητας  σε σχέση με το πρόβλημα των δύο σωμάτων, και η αύξηση είναι πολύ μεγάλη! Η προσθήκη ενός ακόμη σώματος, έστω και ακίνητου, αυξάνει δραματικά την πολυπλοκότητα του προβλήματος, παρότι το πρόβλημα εξακολουθεί να είναι ολοκληρώσιμο.

Ιστορικά, το πρόβλημα των δύο κέντρων μελετήθηκε αρχικά από τον Euler γύρω στο 1760, με την ελπίδα να αποτελέσει ένα ενδιάμεσο βήμα από το πρόβλημα των δύο σωμάτων σε εκείνο των τριών. Το μελέτησε σε δύο διαστάσεις και απέδειξε ότι με τη χρήση ελλειπτικών συντεταγμένων το πρόβλημα διαχωρίζεται (δηλαδή σπάει σε δύο προβλήματα με τους μισούς βαθμούς ελευθερίας το καθένα) και είναι ολοκληρώσιμο (δηλαδή έχει δύο ανεξάρτητες σταθερές συναρτήσεις της θέσης και των ορμής). Οι λύσεις εκφράζονται αναλυτικά με τη βοήθεια των ελλειπτικών συναρτήσεων. Αργότερα, τον 19ο αιώνα, o Jacobi απέδειξε τη διαχωρισιμότητα και την ολοκληρωσιμότητα σε τρεις διαστάσεις. Στο εξαιρετικό βιβλίο του Whittaker (A treatise on the analytical dynamics of particles and rigid bodies), το οποίο μπορεί πλέον να βρει κανείς ελεύθερα στο Internet Archive, αναλύεται το πρόβλημα των δύο κέντρων μέχρι το σημείο όπου οι λύσεις εκφράζονται με τη βοήθεια των ελλειπτικών συναρτήσεων. Από το σημείο όμως αυτό μέχρι το να περιγραφούν και να ταξινομηθούν τα διάφορα ήδη τροχιών η απόσταση είναι πραγματικά πολύ μεγάλη! Δημοσιεύσεις σχετικά με τις διάφορες τροχιές του -κατά τα άλλα απλού και ολοκληρώσιμου- συστήματος των δύο κέντρων έχουν γίνει ακόμα και την τελευταία δεκαετία:
Varvoglis, H., Vozikis, C.H., and Wodnar, K., The Two Fixed Centers: An Exceptional Integrable System, Cel. Mech. Dyn. Astron., 88 (2004), 343-356.
Vaalkens H., Dullin H.R., and Richter P.H., The problem of two fixed centers: bifurcations, actions, monodromy, Physica D 196 (2004), 265-310.

Τυπικές τροχιές

Ας υποθέσουμε λοιπόν ότι έχουμε ένα σημειακό σώμα μάζας m που βρίσκεται στον άξονα x, και βάλλεται όπως φαίνεται στο παρακάτω σχήμα, με ταχύτητα κάθετη στον άξονα x. Το σώμα βρίσκεται υπό τη βαρυτική επίδραση δύο άλλων ακίνητων σημειακών σωμάτων μάζας M το καθένα όπως φαίνεται στο σχήμα.

Αν υπήρχε μόνο ένα από τα σώματα μάζας M, ξέρουμε όλοι ότι για κάθε αρχική ταχύτητα του σώματος μάζας m, η τροχιά θα ήταν κωνική τομή. Αν περιοριστούμε στις δέσμιες τροχιές (δηλαδή εκείνες που δε διαφεύγουν στο άπειρο), η τυπική τροχιά του συστήματος είναι η έλλειψη, με το σώμα μάζας M να βρίσκεται σε μία από τις δύο εστίες αναλόγως με την αρχική ταχύτητα. Τι γίνεται όταν προστεθεί και το δεύτερο σώμα;

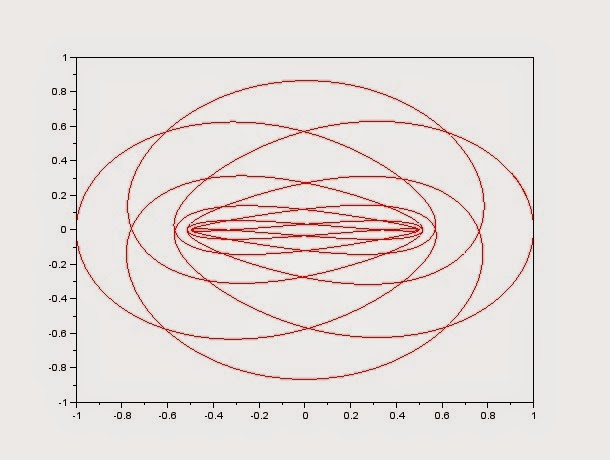
Οι τυπικές τροχιές λοιπόν τότε είναι τροχιές που δεν κλείνουν και γεμίζουν πυκνά μια περιοχή του χώρου. Πυκνά σημαίνει ότι κάποια στιγμή θα περάσουν οσοδήποτε κοντά από οποιοδήποτε σημείο της περιοχής. Το τι σχήμα θα έχει αυτή περιοχή εξαρτάται από την αρχική ταχύτητα, ή πιο αυστηρά από τις τιμές των ολοκληρωμάτων της κίνησης (ποιά είναι αυτά θα τα δούμε στη συνέχεια). Στα παρακάτω σχήματα φαίνονται μια τροχιά από κάθε είδος. Οι αρχικές ταχύτητες είναι 0.8, 1.2 και 1.75 αντίστοιχα. Η αρχική θέση του σωματιδίου είναι x=1, ενώ οι δύο ακίνητες μάζες βρίσκονται στα σημεία με x=-0.5 και x=0.5. Θεωρούμε επίσης G=M=m=1.

Αυξανομένης της ενέργειας έχουμε τρία τυπικά είδη τροχιών:

1. Τροχιές που γεμίζουν πυκνά μια περιοχή που περιλαμβάνει ένα από τα δύο ακίνητα σώματα. Αποδεικνύεται ότι η περιοχή αυτή περιορίζεται από τμήματα μιας έλλειψης και μιας υπερβολής. Στο σχήμα εδώ, δεξιά είναι η έλλειψη και αριστερά η υπερβολή.
2. Τροχιές που γεμίζουν πυκνά μια περιοχή που περιλαμβάνει και τα δύο ακίνητα σώματα. Αποδεικνύεται ότι η περιοχή αυτή περιορίζεται από μία έλλειψη.
3. Τροχιές που γεμίζουν πυκνά έναν δακτύλιο ο οποίος δεν περιλαμβάνει κανένα από τα δύο σώματα. Αποδεικνύεται ότι ο δακτύλιος αυτός βρίσκεται ανάμεσα σε δύο ελλείψεις.

Ένα έμπειρο μάτι εύκολα παρατηρεί ότι οι τροχιές μοιάζουμε με εικόνες Lissajous, δηλαδή με τις εικόνες που λαμβάνουμε από τη σύνθεση δύο ταλαντώσεων με άρρητο λόγο συχνοτήτων σε διευθύνσεις που σχηματίζουν μεταξύ τους κάποια γωνία. Σε ένα διαχωρίσιμο σύστημα η κατάσταση είναι ανάλογη με τις εικόνες Lissajous: ο διαχωρισμός των μεταβλητών ουσιαστικά μετατρέπει το σύστημά μας σε μία σύνθεση δύο ανεξάρτητων συστημάτων. Το πρόβλημα των δύο κέντρων είναι διαχωρίσιμο σε ελλειπτικές συντεταγμένες, γι΄αυτό και τα σύνορα των περιοχών όπου κινείται το σωματίδιο είναι ελλείψεις ή υπερβολές.

Ελλειπτικές τροχιές

Υπάρχουν ελλειπτικές τροχιές με εστίες τις δύο ακίνητες μάζες, όπως εκείνες στο πρόβλημα των δύο σωμάτων; Η απάντηση είναι ναι, και μπορούν να βρεθούν σχετικά εύκολα. Αν υπήρχε μόνο το δεξί σώμα στο x=α, ποιά θα πρέπει να ήταν η αρχική ταχύτητα ώστε το σωματίδιο να διαγράψει έλλειψη με εστίες στα σημεία x=α και x=-α (βλ. σχήμα);

Ξέρουμε ότι η εκκεντρότητα ισούται με τη διαφορά αφηλίου-περιηλίου δια το άθροισμα αφηλίου-περιηλίου:

Από τη σχήμα είναι φανερό ότι

οπότε 

Η εκκεντότητα όμως συνδέεται με την αρχική θέση και ταχύτητα σύμφωνα με τη σχέση:

όπου Ε είναι η ολική ενέργεια:

και L η στροφορμή:

Συνδυάζοντας τις τρεις τελευταίες εξισώσεις και λύνοντας ως προς την αρχική ταχύτητα παίρνουμε:

και αντικαθιστώντας τις τιμές των α και ro παίρνουμε 

Αν υπήρχε μόνο το αριστερό σώμα στο x=-α, ποιά θα πρέπει να ήταν τότε η αρχική ταχύτητα ώστε το σωματίδιο να διαγράψει έλλειψη με εστίες στα σημεία x=α και x=-α (βλ. σχήμα);

Τότε η εκκεντότητα θα ήταν ίδια, ενώ η ολική ενέργεια και η στροφορμή θα ήταν αντίστοιχα:

και λύνοντας με τον ίδιο τρόπο όπως πριν ως προς την αρχική ταχύτητα παίρνουμε:

και αντικαθιστώντας τις τιμές των α και ro παίρνουμε:

Βλέπουμε λοιπόν ότι η ίδια έλλειψη είναι τροχιά του συστήματος με μόνο το δεξί ακίνητο σώμα όσο και με μόνο το αριστερό ακίνητο σώμα, με διαφορετικές όμως αρχικές ταχύτητες. Είναι η έλλειψη αυτή τροχιά του συστήματος και με τα δύο ακίνητα σώματα; Λογικό είναι να υποθέσουμε πως ναι. Και αν ναι με ποιά αρχική ταχύτητα;

Εδώ έρχεται προς βοήθειά μας το θεώρημα του Bonnet, το οποίο αγνοούσα και το έμαθα μέσα από τις σελίδες του Whittaker. Μας λέει το εξής:

Αν μια τροχιά στο χώρο των θέσεων είναι λύση ενός συστήματος με δυναμικό V1 και σε κάποιο σημείο της A η ταχύτητα είναι u1 και η ίδια τροχιά στο χώρο των θέσεων είναι λύση ενός συστήματος με δυναμικό V2 και στο ίδιο σημείο Α η ταχύτητά της είναι u2, τότε η ίδια αυτή τροχιά είναι λύση του συστήματος με δυναμικό V1 + V2 με αρχική ταχύτητα στο σημείο Α:

Έτσι λοιπόν βρίσκουμε ότι ξεκινώντας με αρχική ταχύτητα

βρισκόμαστε πάνω σε μια ελλειπτική τροχιά στο πρόβλημα των δύο κέντρων. Προφανώς η τροχιά αυτή μπορεί να διαγραφεί και κατά την αντίστροφη φορά, επομένως για κάθε αρχική θέση ro έχουμε δύο περιοδικές τροχιές.

Λίγα λόγια για το θεώρημα Bonnet:

Η απόδειξη του θεωρήματος υπάρχει στο βιβλίο του Whittaker (σελίδα 95) αλλά και στο αντίστοιχο λήμμα της Wikipedia. Μπορούμε να το κατανοήσουμε πολύ απλά ως εξής. Ας υποθέσουμε ότι έχουμε δύο κεντρικά πεδία δυνάμεων F1(r) και F2(r) που υποστηρίζουν την ίδια κυκλική τροχιά ακτίνας R με ταχύτητες u1 και u2 αντίστοιχα. Για την κυκλική τροχιά στο πεδίο F1(r), αφού η F1 παίζει το ρόλο της κεντρομόλου δύναμης, ισχύει :

Ομοίως στο πεδίο F2(r):

Αθροίζοντας τις παραπάνω παίρνουμε:

Δηλαδή η κυκλική τροχιά ακτίνας R είναι τροχιά και στο συνδυασμένο πεδίο των F1 και F2 με ταχύτητα ίση με

Εννοείται ότι το θεώρημα του Bonnet γενικεύεται για n πεδία δυνάμεων.

Άλλες περιοδικές τροχιές

Ως τώρα έχουμε βρει για κάθε αρχική θέση δύο περιοδικές τροχιές: μια έλλειψη που διαγράφεται είτε δεξιόστροφα είτε αριστερόστροφα. Επιπλέον, αν το σωματίδιο ξεκινήσει με αρχική θέση και ταχύτητα πάνω στον άξονα y, θα παραμείνει σε αυτόν εκτελώντας ταλάντωση. Αυτό θα συμβεί για οποιαδήποτε αρχική ταχύτητα, επομένως έχουμε μια οικογένεια άπειρων περιοδικών τροχιών στον άξονα y. Σχεδόν προφανές ίσως, καθώς λόγω συμμετρίας, όταν το σωματίδιο βρίσκεται στον άξονα y, η συνισταμένη δύναμη βρίσκεται επίσης σε αυτό τον άξονα. Μπορούμε όμως να πλησιάσουμε την τροχιά (τροχιές ακριβέστερα) αυτή με τις αρχικές συνθήκες που έχουμε διαλέξει; Η απάντηση είναι πως ναι. Τεχνικά: οι ευσταθείς πολλαπλότητες των τροχιών του άξονα y εκτείνονται στην περιοχή δεξιά και αριστερά των ακίνητων σωμάτων καθιστώντας τις τροχιές αυτές προσβάσιμες και μπορούμε να τις ακολουθήσουμε για αρκετές ταλαντώσεις. Ας δούμε δύο χαρακτηριστικά σχήματα. Πρώτα, ας δούμε μια πραγματικά αξιοσημείωτη τροχιά που κάνει το εξής: ενώ ξεκινά στα δεξιά του δεξιού ακίνητου σώματος, το κινούμενο σωματίδιο καταλήγει τελικά να παγιδευτεί στο αριστερό! Στην πορεία διατρέχει πολύ κοντά στον άξονα y για πολλές ταλαντώσεις. Η τροχιά αυτή φαίνεται στο σχήμα που ακολουθεί.

Επιπλέον, όταν η αρχική ταχύτητα είναι στο όριο της μετάβασης από τις τροχιές του τύπου 1 (περιορισμένες στη γειτονιά ενός ακίνητο σώματος) σε εκείνες του τύπου 2 (καλύπτουν πυκνά περιοχή που περιλαμβάνει και τα δύο ακίνητα σώματα), οι τροχιές και πάλι διατρέχουν για αρκετές ταλαντώσεις οσοδήποτε κοντά στον άξονα y. Μία τέτοια τροχιά φαίνεται στο σχήμα που ακολουθεί.

Υπάρχουν άλλες περιοδικές τροχιές; Η απάντηση είναι ναι και είναι άπειρες το πλήθος! Όπως με τις εικόνες Lissajous όπου όταν ο λόγος των συχνοτήτων είναι ρητός έχουμε κλειστές τροχιές, έτσι και στο διαχωρίσιμο σύστημά μας, όταν ο λόγος των συχνοτήτων των δύο υποσυστημάτων είναι ρητός, έχουμε περιοδικές τροχιές.

Στην περίπτωση λοιπόν που οι συχνότητες είναι ίσες έχουμε τις δύο ελλείψεις που βρήκαμε. Η αμέσως ανώτερης τάξης τροχιά είναι μια τροχιά σχήματος 8, όπως φαίνεται στο σχήμα που ακολουθεί.

Υπάρχουν άπειρες ακόμα ανώτερης τάξης περιοδικές τροχιές, όπως εκείνες που φαίνονται στα ακόλουθα σχήματα. Επιπλέον, υπάρχουν σχεδόν κλειστές τροχιές, όπου ο λόγος συχνοτήτων είναι κοντά σε ακέραια τιμή, οι οποίες γεμίζουν πυκνά το διαθέσιμο χώρο. Κάποιες αντιπροσωπευτικές περιοδικές τροχιές φαίνονται στα ακόλουθα σχήματα.

Ειδικά η τελευταία είναι μια πολύ αξιοσημείωτη τροχιά, η οποία περιλαμβάνει δύο σημεία όπου το σωματίδιο σταματάει στιγμιαία! Αυτά είναι το ανώτερο και το κατώτερο σημείο της τροχιάς, όπως φαίνεται στο σχήμα. Το σωματίδιο φτάνει εκεί με μηδενική ταχύτητα και επιστρέφει ακολουθώντας την ίδια τροχιά προς τα πίσω!
Και μια αντιπροσωπειτική σχεδόν κλειστή τροχιά στο σχήμα που ακολουθεί:

Σταθερές της κίνησης

Όπως είπαμε και στην αρχή, το σύστημα των δύο ακίνητων κέντρων είναι ολοκληρώσιμο τόσο στην επίπεδή του εκδοχή (αυτή που μελετάμε εδώ) όσο και στις τρεις διαστάσεις. Στο σύστημα που μελετάμε εδώ, έχουμε δύο σταθερές (ολοκληρώματα) της κίνησης. Η πρώτη είναι η προφανής: πρόκειται για την ολική ενέργεια, αφού η δύναμη προέρχεται από συνάρτηση δυναμικού. Η δεύτερη, και λιγότερο προφανής, είναι η

γνωστή και σαν ολοκλήρωμα Erikson - Hill, που έχει διαστάσεις τετραγώνου στροφορμής. L1 και L2 είναι οι στροφορμές ως προς καθένα από τα δύο κέντρα και οι γωνίες θ1 και θ2 ορίζονται όπως φαίνεται στο παρακάτω σχήμα.

Για α να τείνει στο 0, το σύστημά μας μεταπίπτει σε εκείνο του ενός κέντρου και το ολοκλήρωμα της κίνησης Ω τείνει στο τετράγωνο της στροφορμής, που όπως γνωρίζουμε είναι ολοκλήρωμα της κίνησης για το σύστημα του ενός κέντρου.

Τροχιές σύγκρουσης

Στο πρόβλημα του ενός κέντρου (ή των δύο σωμάτων, το ίδιο είναι ουσιαστικά), σε ότι αφορά την κρούση του κινούμενου σωματιδίου με το ακίνητο, τα πράγματα είναι απλά: οι τιμές της ολικής ενέργειας για τις οποίες θα έχουμε σύγκρουση -θεωρώντας ότι το ακίνητο σώμα έχει πεπερασμένες διαστάσεις και δεν είναι ένα σημείο- βρίσκονται σε ένα περιορισμένο διάστημα τιμών. Ομοίως και ο χρόνος στον οποίο θα συμβεί η κρούση βρίσκεται και αυτός σε ένα πεπερασμένο διάστημα τιμών. Τόσο απλά όσο στο ακόλουθο σχήμα, όπου ένα σωματίδιο ξεκινά με αρχική ταχύτητα uo από ένα σημείο Α, και αφού διαγράψει τμήμα έλλειψης, πέφτει πάνω στο ακίνητο σώμα, του οποίου το κέντρο βρίσκεται πάνω σε μία εστία της έλλειψης.

Αν το μέτρο της αρχικής ταχύτητας αυξηθεί πέρα από μια τιμή, θα έχουμε ελλειπτική τροχιά χωρίς σύγκρουση με το ακίνητο σώμα.

Στην περίπτωση των δύο κέντρων όμως τα πράγματα είναι πολύ διαφορετικά, όπως μπορεί κανείς εύκολα να καταλάβει παρατηρώντας τα σχήματα των τροχιών που γεμίζουν πυκνά περιοχές του χώρου. Οι τροχιές των ειδών 1 και 2 (εκείνες δηλαδή που γεμίζουν πυκνά περιοχές που περιλαμβάνουν το ένα ή και τα δύο ακίνητα σώματα αντίστοιχα), περνούν οσοδήποτε κοντά στο ελκτικό κέντρο. Αυτό σημαίνει ότι όλες οι τροχιές, αργά η γρήγορα και ανεξάρτητα από τις διαστάσεις των ακίνητων σωμάτων, θα συγκρουστούν με κάποιο ακίνητο σώμα. Όσο μικρότερες οι διαστάσεις των ακίνητων σωμάτων, τόσο μεγαλύτεροι θα είναι και οι τυπικοί χρόνοι κρούσης, αλλά το γεγονός της κρούσης είναι μια βεβαιότητα που σίγουρα θα συμβεί αν περιμένουμε αρκετά.

Ας ξεκινήσουμε λοιπόν από το σημείο (0,1) και ας μεταβάλλουμε την αρχική ταχύτητα uo έτσι ώστε να έχουμε τροχιές των τύπων 1 και 2, και ας δούμε πόσος χρόνος θα μεσολαβήσει μέχρι να συγκρουστεί το κινούμενο σώμα με κάποιο από τα ακίνητα. Θεωρούμε την ακτίνα του ακίνητου σώματος ίση με 0.1 ενώ εκείνη του κινούμενου σώματος τη θεωρούμε αμελητέα. Τα αποτέλεσμα φαίνεται στο σχήμα που ακολουθεί.

Ο χρόνος παρουσιάζει ασυνέχειες (τα "σκαλάκια" στη γραφική παράσταση) και τρεις έντονες κορυφές. Οι δύο πρώτες αριστερά που είναι και στενότερες αντιστοιχούν σε σχεδόν κλειστές τροχιές που αργούν να επισκεφθούν τη γειτονιά του ελκτικού κέντρου. Η αριστερή είναι τροχιά του τύπου 1 ("εξερευνά" μια περιοχή γύρω από το ένα κέντρο) ενώ η λίγο δεξιότερη είναι τροχιά του τύπου 2 ("εξερευνά" μια περιοχή που περιλαμβάνει και τα δύο κέντρα). Οι τροχιές αυτές φαίνονται στο παρακάτω σχήμα.

Γενικά, στην περιοχή εκείνη των ταχυτήτων συμβαίνει και η μετάβαση από τροχιές του τύπου 1 σε τροχιές του τύπου 2. Αυτό φαίνεται στο παρακάτω σχήμα όπου φαίνεται με ποιό ακίνητο σώμα γίνεται η κρούση σα συνάρτηση της αρχικής ταχύτητας (Α σημαίνει αριστερό σώμα, Δ σημαίνει δεξί).

Βλέπουμε ότι από την ταχύτητα όπου γίνεται η μετάβαση από τροχιές του τύπου 1 σε εκείνες του τύπου 2, το κινούμενο σώμα μπορεί για ένα εύρος ταχυτήτων να συγκρουστεί με οποιοδήποτε από τα ακίνητα σώματα και μάλιστα με μεγάλη ευαισθησία στις αρχικές σύνθήκες: εκεί όπου η γραφική παράσταση μοιάζει με βούρτσα, με πολύ μικρές αλλαγές (αλλά όχι οσοδήποτε μικρές) στην αρχική ταχύτητα αλλάζει το σώμα με το οποίο θα γίνει η κρούση.

Σε ότι αφορά τη δεύτερη, πλατύτερη και δεξιότερη κορυφή, αυτή αντιστοιχεί στην περιοδική τροχιά σχήματος 8: όσο πιο κοντά σε αυτή ξεκινά το κινούμενο σώμα, τόσο περισσότερο χρόνο χρειάζεται για να "ξεφύγει" από εκείνη και να συγκρουστεί με κάποιο από τα ακίνητα.

Μπορεί να γίνει πιο πολύπλοκο;

Η απάντηση στο ερώτημα είναι πως ναι, και μάλιστα πολύ εύκολα. Αρκεί να αλλάξουμε λίγο τον εκθέτη στο νόμο της δύναμης, δηλαδή πχ από 2 να γίνει 2.02 (βλ, προηγούμενη ανάρτηση για ένα σχετικό προβληματισμό). Τότε η σταθερά της κίνησης Ω πάυει να υπάρχει και το σύστημα γίνεται αυτό που στη φυσική λέμε χαοτικό. Στην περίπτωση αυτή, αν κανείς δει τη γραφική παράσταση χρόνου κρούσης δε θα καταλάβει και μεγάλη διαφορά σε σύγκριση με το αρχικό σύστημα. Αν μεγενθύνει όμως σε συγκεκριμένα σημεία θα καταλάβει τη διαφορά: μεγενθύνοντας συνεχώς παίρνουμε συνέχεια γραφικές παραστάσεις με δομή. Όσο και να μεγενθύνουμε, θα βλέπουμε μια πολύπλοκη δομή, όπως στο ακόλουθο σχήμα.

Παρατηρήστε στο παραπάνω σχήμα την κλίμακα στον άξονα των x: η περιοχή είναι πολύ μικρή καθώς το αρχικό από το τελικό σημείο διαφέρουν στο 5ο δεκαδικό ψηφίο. Μεγενθύνοντας δηλαδή σε καθεμιά συστάδα κορυφών, θα δούμε άλλη μία τέτοια συστάδα, κι αυτό θα συνεχίζεται επ' άπειρο! Τεχνικά, λέμε πως ο χρόνος κρούσης παρουσιάζει ανωμαλίες σε ένα μορφοκλασματικό (fractal) σύνολο πάνω στη γραμμή των αρχικών συνθηκών. Οι ανωμαλίες αυτές οφείλονται στην τομή της γραμμής των αρχικών συνθηκών με τις ευσταθείς πολλαπλότητες των (απείρων σε πλήθος) ασταθών περιοδικών τροχιών. Και μπορούμε να πούμε πάρα πολλά ακόμα πάνω σε αυτό. Γενικά, η αλλαγή του εκθέτη (και γενικότερα της μορφής) του νόμου της δύναμης, επηρεάζει σημαντικά την ευστάθεια βαρυτικών συστημάτων πολλών σωμάτων, και αυτό είναι που ψάχνω περισσότερο αυτό τον καιρό. Αυτό πιθανόν θα είναι το αντικείμενο κάποιας μελλοντικής ανάρτησης.

Επίλογος

Το πρόβλημα των δύο κέντρων είναι ένα πραγματικά εξαιρετικό παράδειγμα με το οποίο μπορεί κανείς να κατανοήσει κάτι πολύ βασικό στη φυσική: ένα απλό σύστημα (όπως αυτό του ενός κέντρου) συν ένα άλλο απλό σύστημα, δε μας κάνουν κάτι απλό ή έστω κάτι 2 φορές πιο σύνθετο. Συνήθως μας κάνουν κάτι απείρως πιο πολύπλοκο, όπως το πρόβλημα των δύο κέντρων. Κάτι επίσης βασικό που μαθαίνουμε είναι ότι διαχωρίσιμο, ολοκληρώσιμο και αναλυτικά επιλύσιμο σύστημα δε σημαίνει απαραίτητα και τετριμμένο. Το πρόβλημα των δύο κέντρων είναι ένα διαχωρίσιμο ολοκληρώσιμο και αναλυτικά επιλύσιμο σύστημα με δύο βαθμούς ελευθερίας, το οποίο όμως παρουσιάζει εξαιρετικά πλούσια συμπεριφορά, η οποία πήρε δεκαετίες για να εξερευνηθεί στην ολότητά της. Και επιπλέον, με μία μικρή αλλαγή στο νόμο της δύναμης, "σπάει" η ολοκληρωσιμότητα και το σύστημα γίνεται χαοτικό.

Τι θα συνέβαινε αν η βαρύτητα δεν ακολουθούσε επακριβώς το νόμο του αντιστρόφου τετραγώνου;

Πως ξέρουμε ότι η δύναμη της βαρύτητας ακολουθεί ακριβώς το νόμο του αντιστρόφου τετραγώνου, δηλαδή πως ξέρουμε ότι ο εκθέτης του r στο νόμο της παγκόσμιας έλξης είναι 2 και όχι πχ 2.00001; Τι θα συνέβαινε τότε; Πως θα μοιάζαν οι τροχιές των πλανητών; 

Αυτή είναι μια ερώτηση που κάνουν συχνά οι υποψιασμένοι μαθητές. Η σύντομη απάντηση που θα μπορούσαμε να δώσουμε είναι πως στα πλαίσια των θεωριών που επιχειρούν να ενοποιήσουν όλες τις δυνάμεις, οι διαστάσεις του χώρου είναι περισσότερες από τρεις και ο νόμος της παγκόσμιας έλξης δε θα πρέπει να ισχύει στη μορφή αυτή σε πολύ μικρές αποστάσεις. Υπάρχουν μάλιστα σε εξέλιξη πειράματα που ερευνούν τις αποκλίσεις της βαρύτητας από το νόμο του αντιστρόφου τετραγώνου αλλά ως τώρα δεν έχει υπάρξει κάποιο αποτέλεσμα στα όρια της ακρίβειας των πειραμάτων.

Αυτό όμως δεν καλύπτει τους μαθητές καθώς αγνοούν τις θεωρίες αυτές και αυτό που πραγματικά θέλουν να μάθουν είναι πως θα επηρέαζε η απόκλιση του εκθέτη από το 2 τις τροχιές σωμάτων που γνωρίζουμε, όπως ο Ηλιος και η Γη. Για το λόγο αυτό, προσπάθησα να γράψω ένα κείμενο που να εξηγεί επακριβώς τις συνέπειες της απόκλισης του εκθέτη από το 2 σε επίπεδο τροχιών. Γράφοντας το κείμενο αυτό ξεκαθάρισα κι εγώ κάποια πράγματα στο μυαλό μου για το ζήτημα. Εδώ θα συνοψίσω απλώς κάποια συμπεράσματα, και για το πλήρες κείμενο παραπέμπω στο τέλος της ανάρτησης. Ας θεωρήσουμε λοιπόν ότι η δύναμη της βαρύτητας ακολουθεί το νόμο

όπου ε ένας μικρός αριθμός, και ας δούμε κάποιες από τις συνέπειες.

Η μορφή των τροχιών

Αν ο εκθέτης του r στο νόμο της παγκόσμιας έλξης ήταν λίγο διαφορετικός από το 2, οι τροχιές δε θα ήταν πλέον κλειστές αλλά τα περιήλια και τα αφήλιά τους θα παρουσίαζαν μετάπτωση. Όσο μεγαλύτερη είναι η απόκλιση του εκθέτη από το 2 τόσο μεγαλύτερη και η γωνιακή τους μετατόπιση ανά περιστροφή. Στο σχήμα που ακολουθεί φαίνεται μια τέτοια τροχιά (με πράσινο χρώμα) η οποία αντιστοιχεί σε ε=0.02. Με κόκκινο χρώμα φαίνεται η ελλειπτική τροχιά που αντιστοιχεί στο νόμο της βαρύτητας με ε=0.

Η κίνηση αυτή, που ονομάζεται μετάπτωση του περιηλίου (και του αφηλίου), είναι συνηθισμένη για τους πλανήτες: το περιήλιο της Γης μεταπίπτει κατά 11.45 δευτερόλεπτα της μοίρας ανά έτος ενώ η αντίστοιχη μετάπτωση για τον Ερμή είναι 5.74. Η μεταπτωτική αυτή κίνηση των πλανητών οφείλεται όχι στην απόκλιση από το νόμο του αντιστρόφου τετραγώνου αλλά στη μεταξύ τους βαρυτική αλληλεπίδραση. Αν η δύναμη δεν ακολουθούσε το νόμο του αντιστρόφου τετραγώνου, θα υπήρχε μια επιπλέον (πολύ μικρότερη συγκριτικά) μετάπτωση στα περιήλια των πλανητών.  Η γωνιακή μετατόπιση του περιηλίου ανά περιστροφή, για μικρές εκκεντρότητες (δηλαδή για τροχιές αρκετά κοντά στην κυκλική), μπορεί εύκολα να αποδειχθεί ότι εξαρτάται από την απόκλιση ε με τη σχέση:

Το περιήλιο του Ερμή, η απόκλιση από το νόμο του αντιστρόφου τετραγώνου, ο πλανήτης Vulcan (Ήφαιστος) και η Γενική Σχετικότητα

Η ιστορία της μετάπτωσης του περιηλίου του Ερμή είναι μια πολύ ενδιαφέρουσα ιστορία που καταδεικνύει με τον καλύτερο πιστεύω τρόπο (και τον προσιτότερο στους μαθητές που δε γνωρίζουν από κβαντομηχανική) την αλλαγή του "παραδείγματος" στα πλαίσια μιας "επιστημονικής επανάστασης" (κατά τον Kuhn). Αξίζει να τη δούμε λίγο σε αυτό το πλαίσιο. Μια πλήρη περιγραφή μπορούμε να βρούμε εδώ: http://www.math.toronto.edu/~colliand/426_03/Papers03/C_Pollock.pdf καθώς και στο βιβλίο In search of planet Vulcan.

Η μετατόπιση λοιπόν του περιηλίου του Ερμή έχει ιδιαίτερη ιστορική σημασία καθώς αποτέλεσε την πρώτη επιτυχή ερμηνεία παρατηρησιακών δεδομένων με τη γενική θεωρία της Σχετικότητας. Ο Ερμής, ο πλησιέστερος προς τον Ήλιο πλανήτης, κινείται σε τροχιά μεγάλης σχετικά εκκεντρότητας (ε=0.206 ενώ εκείνη της γης είναι ε=0.0167) με αποτέλεσμα η θέση του περιηλίου του να μπορεί να προσδιοριστεί με μεγάλη ακρίβεια. Ήδη από τα μέσα του 19ου αιώνα, ενώ είχε ήδη μετρηθεί με ακρίβεια η ταχύτητα μετάπτωσης του περιηλίου του Ερμή, δεν ήταν δυνατό να εξηγηθεί στο συνολό της από τη Νευτώνεια βαρύτητα: υπήρχαν 43 δευτερόλεπτα της μοίρας ανά γήινο αιώνα που ήταν αδύνατο να εξηγηθούν. Για την εξήγησή της απόκλισης αυτής είχε προταθεί η ύπαρξη ενός ακόμα πλανήτη πλησιέστερα στον Ήλιο από τον Ερμή, ο υποθετικός πλανήτης Vulcan (Ήφαιστος δηλαδή, απλή συνωνυμία με την ομώνυμο στο Star Trek), σε απόσταση 0.147ΑU από τον Ήλιο. Καθώς όμως ως το 1890 ο πλανήτης αυτός ήταν ακόμα άφαντος στα τηλεσκόπια των αστρονόμων που τον αναζητούσαν, άρχισε να γίνεται αντιληπτό ότι πρέπει να συμβαίνει κάτι με το νόμο που διέπει τη βαρύτητα. Έτσι, προτάθηκε ότι η βαρύτητα δεν ακολουθεί επακριβώς το νόμο του αντιστρόφου τετραγώνου και ότι εκθέτης του r στον παρονομαστή παρουσιάζει μια απόκλιση περίπου 0.00000016 από την τιμή 2. Στη συνέχεια προτάθηκε ότι ο νόμος της παγκόσμιας έλξης περιέχει και όρους ανώτερης τάξης που επηρεάζουν τη δύναμη σε κοντινές στον ήλιο αποστάσεις. Αυτές όμως οι υποθέσεις παρουσίαζαν προβλήματα καθώς οι συνέπειές τους στην κίνηση των υπολοίπων πλανητών ήταν μη αποδεκτές. Σύντομα όμως, το 1915, ο Einstein έλυσε το πρόβλημα με τη γενική θεωρία της Σχετικότητας δίνοντας έτσι την πρώτη ερμηνεία παρατηρησικών δεδομένων με τη βοήθεια της νέας θεωρίας.

Παρότι τα περισσότερα πειράματα που γίνονται αναζητούν πλέον αποκλίσεις από το νόμο του αντιστρόφου τετραγώνου εκεί όπου οι σύγχρονες θεωρίες ενοποίησης τις περιμένουν, δηλαδή σε αποστάσεις μικρότερες του μέτρου (βλ. πχ εδώ: http://arxiv.org/abs/hep-ph/0307284v1 ή εδώ: http://www.npl.washington.edu/eotwash/sr), φαίνεται ότι το ζήτημα της μετατόπισης του περιηλίου των πλανητών δεν έχει κλείσει: υπάρχουν εργασίες που προσπαθούν να μελετήσουν τυχόν αποκλίσεις από το νόμο του αντιστρόφου τετραγώνου χρησιμοποιώντας νεότερα παρατηρησιακά δεδομένα τα οποία δίνουν επιπλέον μικρές αποκλίσεις στις μετατοπίσεις του περιηλίου κάποιων πλανητών: www.raa-journal.org/raa/index.php/raa/article/viewFile/1597/1347.

Το θεώρημα του κελύφους

Το θεώρημα του κελύφους αποδείχθηκε από το Νεύτωνα και από τα μαθητικά χρόνια μας το χρησιμοποιούμε έστω κι αν δεν έχουμε ακούσει ποτέ το ονομά του. Χάρη σε αυτό, εφαρμόζουμε το νόμο της παγκόσμιας έλξης για σφαιρικά αντικείμενα όπως τους πλανήτες αντιμετωπίζοντάς τους ως να ήταν σημειακές μάζες με όλη τη μάζα τους συγκεντρωμένη στο κέντρο της σφαίρας (ή του κελύφους). Το θεώρημα του κελύφους λέει πως ο νόμος της δύναμης από ένα σφαιρικό κέλυφος ακτίνας r είναι ίδιος με εκείνον αν όλη η μάζα του κελύφους ήταν συγκεντρωμένη στο κέντρο του κελύφους. Επιπλέον στο εσωτερικό του κελύφους η βαρυτική δύναμη μηδενίζεται.

Το θεώρημα του κελύφους ισχύει όταν ο ο εκθέτης του r είναι ακριβώς 2. Επιπλέον, το γεγονός ότι η δύναμη από ένα κέλυφος είναι ανεξάρτητη της ακτίνας του κελύφους, οδηγεί και σε μια άλλη συνέπεια: η δύναμη από μία ομογενή σφαίρα μάζας Μ και ακτίνας R είναι ίση με εκείνη από ένα κέλυφος ίσης μάζας και ακτίνας. Όταν λοιπόν η βαρύτητα ακολουθεί το νόμο του αντιστρόφου τετραγώνου έχουμε

όπου Μ η μάζα του σημείου/κελύφους/σφαίρας και r η απόσταση από το σημείο ή το κέντρο του κελύφους ή της σφαίρας.
Σε περίπτωση όπου ο εκθέτης είναι διαφορετικός του 2, το θεώρημα του κελύφους δεν ισχύει, και η δύναμη από ένα κέλυφος εξαρτάται όχι μόνο από την απόσταση από αυτό αλλά και από την ακτίνα του. Επιπλέον, για εκθέτη μεγαλύτερο του 2, η δύναμη στην επιφάνεια του κελύφους απειρίζεται! Γενικά δηλαδή

Για εκθέτη λοιπόν 2+ε έχουμε:

Οι εκφράσεις γίνονται ιδιαίτερα περίπλοκες και έχουμε και τον απειρισμό στην επιφάνεια του κελύφους και της σφαίρας. Αν επομένως ο εκθέτης ήταν διαφορετικός του 2, θα έπρεπε να χρησιμοποιήσουμε μια εξίσωση σαν την τελευταία για να περιγράψουμε την αλληλεπίδρασης μιας σημειακής (ή θεωρούμενης ως τέτοιας) μάζας με μια σφαιρική κατανομή μάζας, πχ αν θέλαμε να περιγράψουμε την κίνηση της γης γύρω από τον ήλιο. Επιπλέον, επειδή η βαρύτητα από μια σφαιρική κατανομή θα ήταν ισχυρότερη από ίση σημειακή μάζα, θα είχαμε μια επιπλέον μετάπτωση των περιηλίων. Τέλος, αν πάλι θέλαμε να περιγράψουμε την κίνηση δύο σφαιρικών κατανομών μάζας σε σχετικά κοντινή απόσταση μεταξύ τους (πχ ένα σύστημα διπλών αστέρων που βρίσκονται κοντά ο ένας στον άλλο) τότε ούτε η εξίσωση αυτή θα μας έκανε και τα πράγματα θα γίνονταν πολύ πολύ πιο περίπλοκα!

 Το πλήρες κείμενο ακολουθεί παρακάτω. Μπορείτε να το κατεβάσετε σε μορφή pdf από εδώ.

Η κάρτα ήχου ως χρονόμετρο (και όχι μόνο)

1. Εισαγωγή

Αυτό που πάντα προσπαθώ να μεταδόσω στους μαθητές μου είναι ότι ο πειραματισμός δεν είναι κάτι που αρχίζει και τελειώνει στους τέσσερεις τοίχους του σχολικού μας εργαστηρίου. Σε αρκετές μάλιστα περιπτώσεις ούτε καν αρχίζει εκεί λόγω της τραγικής έλλειψης των περισσότερων γυμνασίων σε υλικοτεχνικό εξοπλισμό. Στα λύκεια τα πράγματα είναι πολύ καλύτερα απο πλευράς εξοπλισμού, αλλά ο χρόνος για πειραματισμό στο σχολείο είναι πραγματικά λιγοστός. Συχνά λοιπόν δίνω στους μαθητές που ενδιαφέρονται περισσότερο (σε προαιρετική πάντα βάση) και κάποια πειραματική δουλειά που μπορεί να πραγματοποιηθεί και στο σπίτι με πολύ απλά υλικά ή με κάποιο απλό και δωρεάν λογισμικό. Απλά πειράματα όπως πχ το να μετρηθεί ο συντελεστής τριβής χρησιμοποιώντας ένα χάρακα και ένα κέρμα, να παρασκευαστεί ένα διάλυμα δείκτη (βλ. πχ εδώ) και χαρτάκια εκτίμησης του pH (βλ. πχ. εδώ), να μετρηθεί το ύψος ενός κτιρίου ή το βάθος ενός πηγαδιού με το πέταγμα μιας πέτρας, να μετρηθεί η περίοδος ενός εκκρεμούς και να μελετηθεί πως την επηρεάζει πχ η αλλαγή μιας παραμέτου όπως το μήκος του νήματος κλπ.

Όλοι σχεδόν οι μαθητές έχουν στο σπίτι τους έναν υπολογιστή εφοδιασμένο με ένα πολύ χρήσιμο εργαλείο συλλογής δεδομένων. Αυτό δεν είναι άλλο από την κάρτα ήχου. Η πρώτη φορά που χρησιμοποίησα την κάρτα ήχου στο σχολικό εργαστήριο ήταν το σχολικό έτος 2007-2008 στη Γ΄Λυκείου (βλ. εδώ και εδώ), όπου αντικατέστησε τη γεννήτρια συχνοτήτων και τον παλομογράφο. Το κερδος σε χρόνο ήταν τεράστιο αλλά και αποφύγαμε τις περιττές για την ουσία του πράγματος λεπτομέρειες που αφορούν τη σύνδεση και τη χρήση των γεννητριών και των παλμογράφων, χώρια που γλιτώσαμε το δέος που προκαλούν στους μαθητές τα δεκάδες κουμπιά ενός παλμογράφου.

2. Το πρόβλημα

Εδώ θα περιγράψω μια άλλη εφαρμογή της κάρτας ήχου, κατάλληλη τόσο για το εργαστήριο όσο και για το σπίτι: εκείνη της χρονομέτρησης γεγονότων που συνδέονται με κάποιον ήχο, όπως η αναπήδηση μας μπάλας στο έδαφος, η ελεύθερη περιστροφή του πίσω τροχού ποδηλάτου που κάνει το χαρακτηριστικό τσικ-τσικ κλπ. Ας χρησιμοποιήσουμε τη μπάλα που αναπηδά ως παράδειγμα. Όλοι ξέρουμε ότι μια μπάλα που αναπηδά στο έδαφος χάνει σε κάθε κρούση της ένα ποσοστό της ενέργειάς της. Έτσι, μετά από κάθε αναπήδηση ανέρχεται σε μικρότερο ύψος από την προηγούμενη ενώ οι χρόνοι μεταξύ δύο κρούσεων στο έδαφος γίνονται όλο και μικρότεροι. Το ερώτημα λοιπόν είναι: μπορούμε με κάποιο τρόπο να εκτιμήσουμε το ποσοστό της ενέργειας που χάνει σε μια κρούση; Είναι το ποσοστό αυτό σταθερό ή έστω σχεδόν σταθερό καθώς η μπάλα πραγματοποιεί διαδοχικές κρούσεις με το έδαφος;

Αν πριν κάποια κρούση (ας την πούμε n), η ενέργεια της μπάλας είναι En, μετά την κρούση είναι En+1, και με α συμβολίσουμε το λόγο En+1/En, τότε τα αντίστοιχα ύψη αναπήδησης πριν και μετά την κρούση σχετίζονται ως εξής:

ενώ για τα αντίστοιχα χρονικά διαστήματα ισχύει:

Το ποσοστό επομένως της ενέργειας που χάνεται στην κρούση είναι:

Οι συμβολισμοί εξηγούνται στο σχήμα που ακολουθεί. Τις παραπάνω σχέσεις είναι πολύ εύκολο να της αποδείξει ένας μαθητής που έχει διδαχθεί ποσοτικά την έννοια της ενέργειας (διδάσκεται στο δεύτερο τετράμηνο της Α' τάξης του Λυκείου). Εννοείται ότι έχουμε αγνοήσει τη συνεισφορά του αέρα και της στροφορμής που αποκτά η μπάλα στην απώλεια ενέργειας.

Επομένως αν μετρήσουμε δύο διαδοχικά χρονικά διαστήματα Δt μεταξύ κρούσεων μπορούμε να υπολογίσουμε το συντελεστή α και κατ' επέκταση το ποσοστό απώλειας ενέργειας  λ σε κάθε κρούση.

3. Η λήψη των μετρήσεων

Πως θα μετρήσουμε λοιπόν αυτά τα χρονικά διαστήματα που καθώς περνά ο χρόνος γίνονται όλο και μικρότερα; Εδώ λοιπόν θα χρησιμοποιήσουμε την κάρτα ήχου η οποία είναι και σε αυτή την περίπτωση ένα πολύτιμο βοήθημα. Αφήνουμε τη μπάλα να πέσει από κάποιο ύψος και καταγράφουμε τον ήχο που κάνει η μπάλα με ένα μικρόφωνο συνδεδεμένο στον υπολογιστή ή ακόμα και με ένα smartphone. Το τελευταίο μάλιστα έχει το πλεονέκτημα ότι μπορούμε να το πλησιάσουμε πολύ στην πηγή του ήχου και να τον καταγράψουμε καλύτερα, με κόστος λίγη επιπλέον προσπάθεια για τη μεταφορά και την εισαγωγή των δεδομένων στον υπολογιστή. Το λογισμικό που συστήνουμε να χρησιμοποιηθεί για την ηχογράφηση είναι το Wavosaur. Πρόκειται για ένα λογισμικό που παρέχεται δωρεάν (βλ. www.wavosaur.com για κατέβασμα), έχει τη δυνατότητα να ηχογραφεί από το μικρόφωνο και μετά τη λήξη της εγγραφής μας εμφανίζει στην οθόνη την κυματομορφή του ηχητικού αποσπάσματος που ηχογραφήσαμε. Ας δούμε λοιπόν στο Wavosaur την κυματομορφή που καταγράφεται κατά την αναπήδηση μιας μπάλας.

 

Κάθε κρούση της μπάλας με το έδαφος αντιστοιχεί με μια ταλάντωση που φθίνει γρήγορα. Το σημείο έναρξης αυτής της ταλάντωσης (που σχεδόν συμπίπτει και με την κορυφή) αντιστοιχει στην κρούση της μπάλας με το έδαφος. Τις χρονικές στιγμές που έχουμε κρούση μπορούμε να τις προσδιορίσουμε μετακινώντας τον κέρσορα (στην εικόνα παραπάνω αντιστοιχεί στην κατακόρυφη γραμμή αριστερά) πάνω στις κορυφές. Ο αντίστοιχος χρόνος φαίνεται στο πεδίο κάτω δεξιά. Έτσι, μπορούμε να καταγράψουμε τις χρονικές στιγμές που γίνονται τουλάχιστο οι πρώτες οι κρούσεις 17 κρούσεις. Από την 17η και άνω, η ένταση του σήματος είναι μικρή και χάνεται μέσα στο θόρυβο του περιβάλλοντος. Έτσι λοιπόν παίρνουμε 17 τιμές του χρόνου για τις κρούσεις. Με μια καλύτερη και πιο καλά φουσκωμένη μπάλα μπορούμε να πάρουμε περισσότερες.

Εναλλακτικές για τη συλλογή των δεδομένων:

• Σε περίπτωση χρήσης smartphone, το αρχείο m4a που θα προκύψει μπορούμε να το μετατρέψουμε σε wav (ώστε να ανοίγει από το Wavosaur) με το πρόγραμμα Freemore WMA to MP3 converter.
• Για τη μελέτη της κυματομορφής υπάρχουν και τα προγράμματα WASP και BROWSE, και τα δύο από το τμήμα Speech, Hearing and Phonetic Sciences του UCL. Το πρώτο από τα προγράμματα αυτά έχει τη δυνατότητα εγγραφής ενώ το δεύτερο όχι. Αξίζει μια επίσκεψη στη σελίδα του τμήματος (http://www.phon.ucl.ac.uk/resource/software.php) όπου μπορούμε να βρούμε πολύ χρήσιμα δωρεάν προγράμματα για τη μελέτη του λόγου αλλά και του ήχου γενικότερα. Από αυτά ξεχώρισα το RTSPEC το οποίο κάνει ανάλυση φάσματος σε πραγματικό χρόνο και την εμφανίζει στην οθόνη ταυτόχρονα με την κυματομορφή, σε αντίθεση με το Scope  που χρησιμοποιούσα ως τώρα όπου φάσμα και κυματομορφή εμφανίζονται σε ξεχωριστά παράθρα.

4. Επεξεργασία των δεδομένων

 Από τις τιμές του χρόνου που έχουμε, βρίσκουμε τα χρονικά διαστήματα αφαιρώντας από κάθε τιμή χρόνου την προηγούμενή της. Από τα χρονικά διαστήματα, διαιρώντας καθένα με το προηγούμενό του και υψώνοντας το αποτέλεσμα στο τετράγωνο βρίσκουμε το συντελεστή α, από όπου προκύπτει και ποσοστό απώλειας ενέργειας κατά την κρούση λ = 1 - α. Τα παραπάνω τα δείχνουμε σχηματικά πάνω στην κυματομορφή (ζουμαρισμένη στο Wavosaur) για τις λίγες πρώτες κρούσεις.

Βλέπουμε ότι το ποσοστό απώλειας διακυμαίνεται μεταξύ ~21 και ~28% σε αυτές τις πρώτες κρούσεις. Μπορούμε να γίνουμε και πιο αναλυτικοί (αναλόγως του επιπέδου και της διάθεσης των μαθητών να ασχοληθούν) και να καταχωρήσουμε τα αποτελέσματά μας σε έναν πίνακα σαν τον παρακάτω, με πλήθος γραμμών όσες και οι κρούσεις που καταφέραμε να ηχογραφήσουμε. Παραλείποντας λεπτομέρειες και αριθμούς, εμείς υπολογίσαμε μια μέση τιμή ~0.18 για το λ, με σαφή τάση μείωσης καθώς αυξάνεται ο αριθμός των κρούσεων. Πιθανώς η μείωση αυτή να οφείλεται στο ότι η μπάλα επιβραδύνεται και η αντίσταση του αέρα μειώνεται. Η μπάλα μας ήταν αρκετά ελαφριά για τον όγκο της και πιθανόν η αντίσταση του αέρα να μην ήταν αμελητέα. Αν κάποιος επαναλάβει το πείραμα ας με ενημερώσει αν παρατήρησε αυτή τη μείωση του λ.

Για προχωρημένους: Αν συμβολίσουμε με to το πρώτο χρονικό διάστημα, τότε το n-στο δίνεται από τη σχέση:

Επομένως αν παραστήσουμε γραφικά το λογάριθμό του tn σα συνάρτηση του n, θα λάβουμε σημεία τα οποία θα προσεγγίζουν μια ευθεία με κλίση (loga)/2 αν ο συντελεστής α είναι σταθερός. Αν όχι, η κλίση της καμπύλης που ορίζουν τα σημεία θα γίνεται λιγότερο απότομη καθώς ο α αυξάνεται. Στη δική μας περίπτωση η γραφική παράσταση δείχνει όπως στο παρακάτω σχήμα.

 

Με προσαρμογή ελαχίστων τετραγώνων βρίσκουμε μια ευθεία με κλίση -0.0432 που αντιστοιχεί σε α=0.819 ή λ=0.181. Όπως όμως φαίνεται από τα σημεία στο παραπάνω σχήμα η τιμή αυτή για το λ είναι απλώς μια μέση τιμή. Η καμπύλη γίνεται λιγότερο απότομη καθώς το n αυξάνεται, που σημαίνει -όπως είδαμε και προηγουμένως- ότι η απώλεια ενέργειας γίνεται μικρότερη.

5. Τι ακόμα μπορούμε να κάνουμε με την κάρτα ήχου

Μπορούμε να κάνουμε πραγματικά πολλά πράγματα, αν έχουμε κάποιες γνώσεις προγραμματισμού και ηλεκτρονικών. Για οτιδήποτε άλλο εκτός από τη σύνδεση μικροφώνου χρειάζεται να ληφθεί ειδική μέριμνα με την κατασκευή κάποιου είδους interface για να μην ξεπεραστεί η μέγιστη τάση εισόδου, η οποία μάλιστα διαφέρει σημαντικά από κάρτα σε κάρτα. Ίσως για το λόγο αυτό δεν υπάρχουν τυποποιημένοι αισθητήρες για χρήση στην υποδοχή του μικροφώνου (με εξαίρεση δύο αισθητήρες θερμοκρασίας για το iPhone: iCelsius και Thermodo με κόστος $47 και $30 αντίστοιχα, ο πρώτος έχει και εξάρτημα για barbeque...). Ψάχνοντας στο διαδίκτυο βρήκα ένα μεγάλο πλήθος εφαρομογών της κάρτας ήχου, με πιο ενδιαφέρουσες κατά τη γνώμη μου τις παρακάτω:

• Ένας απλός, φτηνός αλλά αποτελεσματικός σεισμογράφος:http://motivationtolearn.org/wordpress/?p=1100
• Φωτοπύλες: http://arxiv.org/ftp/arxiv/papers/1103/1103.1760.pdf
• Μετρητής LCR κόστους δύο λιρών: http://icom.hsr.ch/fileadmin/user_upload/icom.hsr.ch/publikationen/RLC_Meter_EN.pdf
• Καταγραφή ηλεκτροκαρδιογραφήματος: http://www.hobbielektronika.hu/forum/getfile.php?id=77848 και http://arxiv.org/ftp/arxiv/papers/1402/1402.3651.pdf.
• Μέτρηση αντίστασης και θερμοκρασίας με θερμίστορ: http://dc.ee.ubm-us.com/i/43174/58.
• Λήψη κυμάτων VLF: http://www.qsl.net/dl4yhf/speclab/vlf_rcvr.htm .
• Μερικές ιδέες για πειράματα με φωτοπύλες και ωμόμετρο: http://arxiv.org/ftp/arxiv/papers/1108/1108.1109.pdf .
• Ένα interface για παλμογράφο ώστε να εισάγουμε όποιο σήμα θέλουμε στην κάρτα ήχου χωρίς να κινδυνεύουμε να την καταστρέψουμε: http://www.instructables.com/id/Use-Your-Laptop-as-Oscilloscope.

Η κατασκευή των παραπάνω μπορεί να γίνει φθηνά και γρήγορα από κάποιον που γνωρίζει βασικά ηλεκτρονικά. Ακόμα μπορεί κάποια από αυτές τις κατασκευές να αποτελέσει μέρος ενός μικρού project για μαθητές της τεχνικής εκπαίδευσης της αντίστοιχης κατεύθυνσης.

Ιδέα για πείραμα: Από τον ήχο που κάνει ο πίσω τροχός ενός ποδηλάτου μπορούμε να προσδιορίσουμε τη γωνιακή ταχύτητα και επιτάχυνση, αναλύοντας τον ήχο (το χαρακτηριστικό τσίκι-τσίκι) στο Wavosaur. Μπορούμε επομένως να υπολογίσουμε τη ροπή αδράνειάς του αν τον μετατρέψουμε σε τροχαλία τυλίγοντας στην περιφέρειά του ένα σκοινί με αναρτημένο ένα γνωστό βάρος και αφήνοντάς τον να επιταχυνθεί από το βάρος του σώματος. Μπορούμε επιπλέον να υπολογίσουμε εύκολα το πως η τριβή των ρουλεμάν επηρεάζει το παραπάνω αποτέλεσμα μετρώντας τη γωνιακή του επιτάχυνση ενώ αυτός περιστρέφεται χωρίς το βάρος. Περισσότερα σε επόμενη ανάρτηση.